Hoe ver kun je een meteoor zien?
>Ik krijg e-mail.
De meeste stellen verschillende soorten vragen, waarvan de meeste redelijk eenvoudig te beantwoorden zijn (in feite kan veel worden beantwoord door te googlen, hint hint). Maar soms krijg ik een vraag die moeilijker te beantwoorden is, of zelfs een vraag die ik me over mezelf heb afgevraagd, maar die ik nooit heb kunnen achterhalen.
geest in de schaal leeftijdsclassificatie
Dus ik was behoorlijk geïntrigeerd toen ik een vraag kreeg van Bad Reader Dean Lewis over meteoren. Tijdens de Perseïden meteorenregen in 2018 was hij weg van zijn familie, ongeveer 1.000 kilometer van elkaar gescheiden. Als hij een meteoor zag, was het dan mogelijk dat ze dezelfde vanuit hun verder verwijderde locatie konden zien?
Het korte antwoord is: Ja! Het lange antwoord is ... wiskunde. Coole, leuke wiskunde.
En aangezien, wanneer dit artikel wordt gepost, de jaarlijkse Geminid meteorenregen van 2018 vanavond piekt, denk ik dat het gepast is om dit uit te zoeken.
Spoedcursus astronomie: meteoren, meteoroïden en meteorieten, oh my!
Als de aarde perfect plat zou zijn, zou je in principe een meteoor tot aan elke rand van de aarde kunnen zien. Zolang je boven de grond bent, zelfs maar een heel klein beetje, dan bereikt je gezichtslijn elke vierkante centimeter van de planeet aan jouw kant, zodat elke meteoor voor iedereen zichtbaar is. In werkelijkheid is de lucht niet perfect transparant, dus op enige afstand kijk je door zoveel modder dat je niets kunt zien.
De aarde is echter niet plat. Ernstig! Het is rond. En de atmosfeer omringt het als een schelp, wordt dunner met de hoogte en vervaagt uiteindelijk; die hoogte hangt af van uw definitie van ruimte. We kunnen echter een beetje vals spelen omdat we de wetenschap kennen: meteoren zoals die in buien hebben de neiging om ongeveer 100 kilometer boven de grond te verbranden. Die hoogte hangt van veel dingen af, waaronder hoe groot de meteoroïden (de vaste stukjes interplanetair puin die door de ruimte razen) zijn, hoe snel ze bewegen, onder welke hoek ze de atmosfeer binnenkomen, enzovoort. Maar laten we het 100 km noemen.
Het dichtst bij een meteoor kan zijn als je er direct onder staat, en dan is het 100 km recht omhoog (op je zenit). Als het verder van het zenit afbrandt, dan moet het verder van jou af zijn. Het verst weg dat je een meteoor kunt zien, is logisch, dus als hij precies aan de horizon staat.
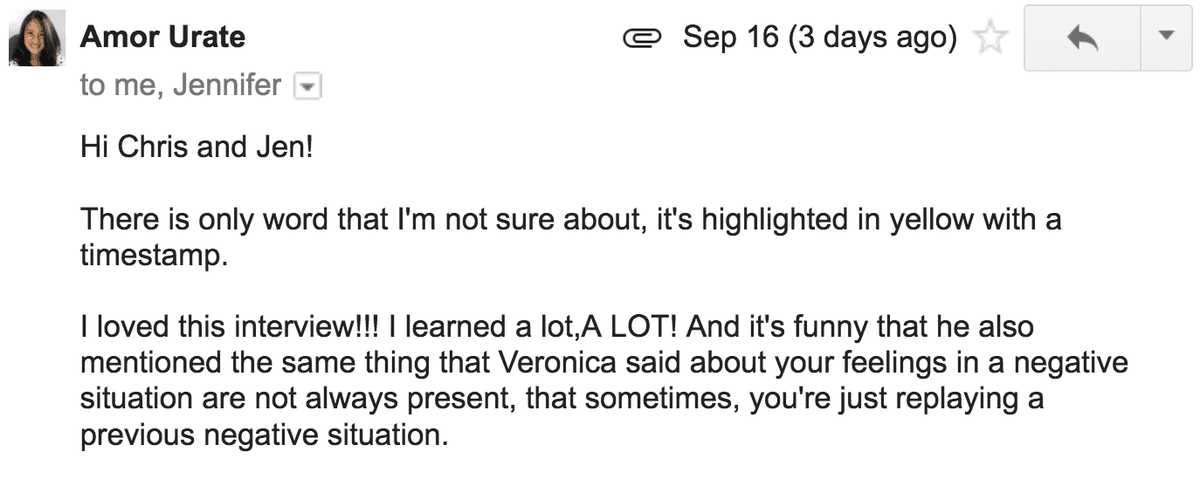
De geometrie ervan ziet er als volgt uit (let op: NIET op schaal):
Schematische weergave van de geometrie van een waarnemer die een meteoor ziet opbranden. Krediet: Phil Plait
Je kunt het kleine stokfiguurtje van de mens zien staan op het oppervlak van de gebogen aarde - laten we zeggen dat jij het bent - met de (ook gebogen) atmosfeer erboven. In dit diagram is R de straal van de aarde (6.4000 km), h is de hoogte waarop de meteoor verbrandt (100 km), en d is de afstand van jou tot de meteoor. A is de hoek tussen je positie op de aarde en de positie van de meteoor erboven, en cursief l (zoals in lengte) is de afstand die je zou moeten lopen om de meteoor recht boven je hoofd te hebben (ik weet dat dat raar lijkt willen weten, maar geduld met me hebben). Vreemd genoeg kun je hier alles berekenen wat je nodig hebt zonder d te weten, maar kom op, het is cool om te weten hoe ver de meteoor is, toch?
De sleutel tot dit alles is om te zien dat de hoek tussen de meteoor, jou en het middelpunt van de aarde een rechte hoek is. Dat komt omdat de meteoor zich aan de horizon bevindt zoals jij hem ziet (of, als je de voorkeur geeft aan grappig jargon, op de raaklijn op de binnenste cirkel waar R hem snijdt). Dat maakt de driehoek tot een rechthoekige driehoek, en als je je wiskunde op de middelbare school herinnert, betekent dat dat je alle zijden en hoeken kunt vinden!
Herinneren de stelling van Pythagoras ? In een rechthoekige driehoek is het kwadraat van de lengte van de hypotenusa gelijk aan de som van de kwadraten van de andere twee zijden*. In onze driehoek is de hypotenusa R+h, en de andere zijden zijn R en d.
Dus
(R+h)2= d2+ R2
of, door de linkerkant te vermenigvuldigen (gebruik FOLIE ):
R2+ 2Rh + h2 = d2+ R2
Los op voor d om te zien hoe ver de meteoor van je verwijderd is. Merk op dat R2 aan beide kanten is, dus annuleer ze om te krijgen
NS2= 2Rh + h2
Of
d = vierkantswortel (2Rh + h2)
Nou, we kennen al die cijfers! Plug-n-chug, schat:
d = vierkantswortel (2 x 6.400 x 100 + 10.000) = 1.136 km
Aha! Dit betekent dat als je een meteoor aan de horizon ziet, deze meer dan 1100 kilometer verwijderd is! Dat is een lange weg, en technisch gezien is het verste weg dat je een meteoor vanaf de grond kunt zien.
Laten we nu de cursieve l zoeken. Eerst moeten we de hoek A weten. Dat vereist wat trigonometrie. Er zijn veel van trig identiteiten je kunt gebruiken om dit uit te zoeken, maar mijn favoriet†is dat in een rechthoekige driehoek de sinus van een hoek de lengte is van de overstaande zijde gedeeld door de lengte van de hypotenusa. Dus als we die verhouding krijgen, kunnen we de inverse sinus (of boogsinus) nemen om de hoek te krijgen.
zonde (A) = d / (R + h)
dus
A = zonder-1(d / R + uur)
Plug-n-chug weer, en ik krijg A = 10°. Dat is een behoorlijk stuk van het aardoppervlak!
En nu kunnen we cursieve l krijgen. Er zijn 360° rond de aarde, en de omtrek van de aarde is 2 x pi x straal = 40.192 km, dus er zijn
40.192 km / 360° = 112 kilometer per graad
wat op zijn beurt 10° = 1120 kilometer betekent. Dat is vrij dicht bij d, wat niet zo verwonderlijk is. De tekeningen zijn overdreven, maar in werkelijkheid is de luchtschil boven ons klein in vergelijking met de grootte van de aarde. Als ik de tekeningen op schaal zou maken, zou je zien dat d en ik qua lengte behoorlijk dicht bij elkaar liggen.
Oké, dus waarom ben ik zo opgewonden en gehinderd voor het vinden van mij? Vanwege de oorspronkelijke vraag! Als je het na al die wiskunde bent vergeten, hoe ver kunnen twee mensen dan zijn en nog steeds dezelfde meteoor zien?
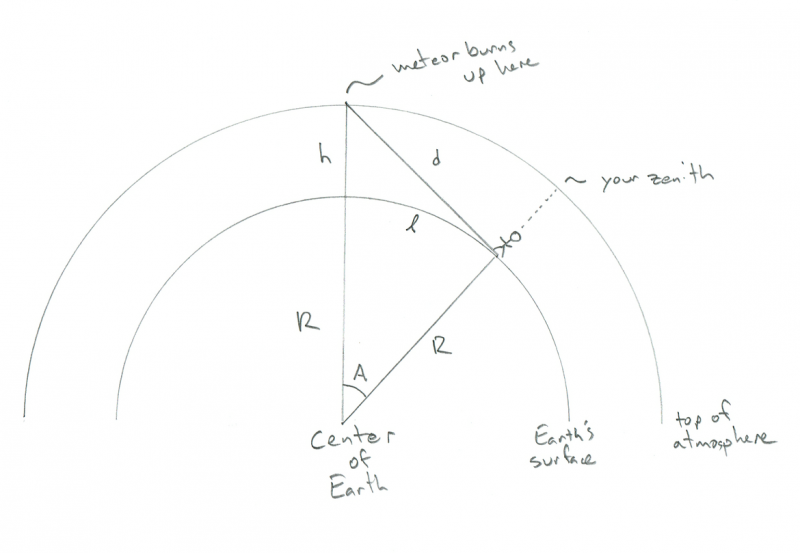
Welnu, in dat geval zou de meteoor direct tussen hen in zijn, en op elk van hun respectieve horizonten. Die geometrie ziet er als volgt uit:
Schematische weergave van de geometrie van twee waarnemers die een meteoor precies tussen hen in zien opbranden. Krediet: Phil Plait
AHA! Nu snap je waarom ik ik wil! De afstand tussen de twee personen is slechts 2 x l! Dus nu hebben we het antwoord:
Als twee mensen dezelfde meteoor kunnen zien, mogen ze niet meer dan 2 x 1.120 = 2.240 kilometer van elkaar verwijderd zijn. Dat is bijvoorbeeld vrij dicht bij de afstand tussen Washington, DC en Denver. Wauw.
Overigens, voor een verandering van perspectief (letterlijk), betekent dit vanuit het gezichtspunt van de meteoor, dat hij een stuk aarde van 2.240 kilometer breed kan zien (zoals in, DC op de oostelijke rand van de aarde en Denver op de westelijke). Dat is best wel cool.
En dat brengt ons bij het eigenlijke antwoord op Dean's vraag: als hij 1000 km van zijn familie verwijderd was, ja, technisch gezien zouden ze dezelfde meteoor kunnen zien. Wat vind je ervan?
mier man en de wesp ouders gids
Dit veronderstelt weer dat de lucht volkomen helder is en zo, wat in werkelijkheid in wezen onmogelijk is. Dus deze wiskunde vertegenwoordigt een ideale situatie (inclusief het idee dat de meteoor er precies tussenin staat).
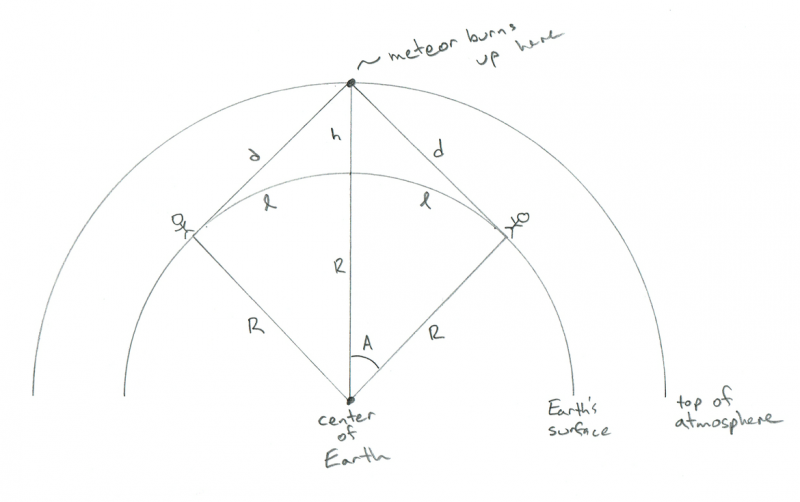
Laten we realistischer zijn. Laten we zeggen dat de meteoor voor beide waarnemers in de lucht opbrandt op een hoogte van 45° boven de horizon. Hoe ver zouden ze van elkaar verwijderd zijn? Welnu, ervan uitgaande dat de meteoor er precies tussen zit, is de geometrie meer als volgt:
Schematische weergave van de geometrie van een waarnemer die kijkt naar een meteoor die 45° boven de horizon opbrandt. Krediet: Phil Plait
Dit is eigenlijk moeilijker op te lossen, maar ik ken nog een truc: als we aannemen dat l klein is, dan is de kromming van de aarde niet belangrijk. Als ik bijvoorbeeld de afstand tussen twee bomen in mijn tuin wil weten, maakt het mij niet uit dat de aarde gebogen is. Over zo'n kleine afstand kan ik aannemen dat het vlak is. Laten we die veronderstelling hier maken.
In dat geval hebben we nog een rechthoekige driehoek, maar deze keer is de rechte hoek die onder de meteoor. Ik heb het zelfs in het diagram gelabeld met het kleine vierkante notatie-dingetje. Dus als dat een hoek van 90° is, en onze hoek met de meteoor is 45°, dan is de laatste hoek (van de meteoor tot de waarnemer) ook 45°. Dat betekent dat dit een gelijkbenige driehoek moet zijn, dus l en h zijn hetzelfde! Omdat we weten dat h 100 km is, moet l ook.
En dat betekent dat de afstand tussen onze twee waarnemers twee keer zo groot is, ofwel 200 km.
Overigens is in dit geval de afstand tot de meteoor ongeveer 141 km. De bevestiging daarvan laat ik als oefening aan de lezer over.
In principe betekent dit dat als je weet hoe hoog een meteoor boven de horizon staat en op welke hoogte hij is opgebrand, je de afstand kunt berekenen (of als je de afstand weet, kun je de hoogte bepalen). Die trig is echter behoorlijk ingewikkeld en ik denk dat ik je voor vandaag genoeg wiskunde heb gegeven.
Maar het is cool om te bedenken dat een beetje wiskunde op de middelbare school zo'n leuke toepassing kan hebben. En ik geef toe dat het poëtisch en romantisch is om te weten dat, zolang de scheiding niet te ver is, het mogelijk is om het zien van een vallende ster met iemand anders te delen. Wat een mooie gedachte.
* In De tovenaar van Oz , de vogelverschrikker had dit verkeerd na hij heeft hersens.
† Van Cursus Ik heb een favoriete trig-identiteit. Wat is van jou?